Radix sort algorithm implementation in C programming

Radix sort in an intuitive non-comparative integer title sorting algorithm Radix sort puts the elements in order by comparing the individual digits of the numbers which share the same significant position and value. Radix type processes the digits either by the Least Significant Digit (LSD) method or the Most Significant Digit (MSD) method.

Radix sort algorithm implementation in C programming

The algorithm of Radix sort follows the following pattern :

• Receive an unsorted array of integers, often referred to/represent a key.
• Iterate from most to least (or least to most) significant digits.
• Each iteration sorts all of the current considerable number of values in the array.

* A key is symbolized as an integer value associated with other data, such as birth date, location, etc.

There are two classifications of Radix sorting :

1. LSD Radix sort.
2. MSD Radix sort.

LSD radix sorts typically use short keys that come before longer keys, and keys of the same length are sorted lexicographically. This coincides with the normal order of integer representations, A sequence as " 2,9,3,4,7,5,6,1,8,10" and after sorting the sequence 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. And for words, A sequence such as "b, c, d, e, f, g, h, i, ba" would be lexicographically sorted as "ba, b, c, d, e, f, g, h, i."

MSD radix sorts use lexicographic order, suitable for sorting strings, such as words, or fixed-length integer representations. A sequence such as "b, c, d, e, f, g, h, i, ba" would be lexicographically sorted as "b, ba, c, d, e, f, g, h, i." And for variable-length integer representation, A sequence as “ 2,9,3,4,7,5,6,1,8,10”and after sorting the sequence 1,10, 2, 3, 4, 5, 6, 7, 8, 9 .

Suppose we have 9 numbers:

493   812   715   710   195   437   582   340   385

After Sorting, it should look like this:

195   340   385   437   493   582   710   715   812

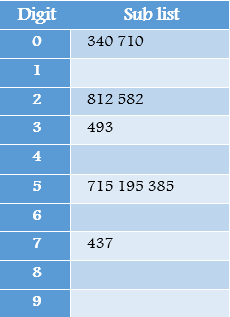
We should start sorting by comparing and ordering the one's digits:

Notice that the numbers were added to the list in the order that they were found, which is why the numbers appear to be unsorted in each of the sublists above. Now, we gather the sublists (in order from the 0 sub-list to the 9 sub-list) into the main list again:

340   710   812   582   493   715   195   385   437

Note: The order in which we divide and reassemble the list is essential, as this is one of the foundations of this algorithm.
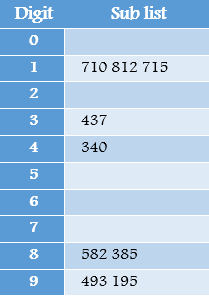
Now, the sublists are created again, this time based on the ten's digit:

Now the sublists are gathered in order from 0 to 9:

710   812   715   437   340   582   385   493   195

Finally, the sublists are created according to the hundred's digit:

At last, the list is gathered up again:

195   340   385   437   493   582   710   715   812

The C Code using LSD Radix sort Algorithm is below:

/* Sort an Integer Array using LSD Radix Sort Algorithm */ #include <stdio.h> int min = 0, count = 0, array[100] = {0}, array1[100] = {0}; void main() { int k, i, j, temp, t, n; printf("Enter size of array :"); scanf("%d", &count); printf("Enter elements into array :"); for (i = 0; i < count; i++) { scanf("%d", &array[i]); array1[i] = array[i]; } for (k = 0; k < 3; k++) { for (i = 0; i < count; i++) { min = array[i] % 10; /* To find minimum LSD */ t = i; for (j = i + 1; j < count;j++) { if (min > (array[j] % 10)) { min = array[j] % 10; t = j; } } temp = array1[t]; array1[t] = array1[i]; array1[i] = temp; temp = array[t]; array[t] = array[i]; array[i] = temp; } for (j = 0; j < count; j++) /*to find MSD */ array[j] = array[j] / 10; } printf("Sorted Array (Using LSD Radix sort) : "); for (i = 0; i < count; i++) printf("%d ", array1[i]); }

Radix Sort is very simple, and a computer can do it fast. When it is appropriately programmed, Radix Sort is, in fact, one of the fastest sorting algorithms for numbers or strings of letters. But sometimes, it does not sort in place. Running Time of Radix sort is O (d (n+k)), where n is the number of elements, k is the number of bits per element, and d is a digit.

Related Post :

Bubble sort in javaTopological sort of directed graph in java

Binary search in C Binary search in java

Breadth-First Search ( BFS ) in java death First Search ( DFS ) in java

Introduction to algorithm,3rd edition Programming in ANSI C by Balagurusamy