RSA Algorithm (Encryption and Decryption) implementation in C

The RSA algorithm is a public key encryption technique used widely in network communication, like Virtual Private Networks (VPNs), to secure sensitive data, particularly when sent over an insecure network such as the Internet.

RSA algorithm was first described in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman of the Massachusetts Institute of Technology.

In a cryptosystem, the system must ensure that nobody, except the intended recipient, deciphers the message. The people involved had to strive to keep the key secret. In public-key encryption techniques, a key is split into two, called public and private keys. A public key is advertised worldwide, and the private key is kept secret. It is not possible to generate a private key using the public key. Someone who knows the public key cannot decrypt a message after it has been encrypted using the public key. Working with a public-key encryption system has mainly three steps: 

1. Key generation: Whoever wants to receive secret messages creates a public key (published) and a private key (kept secret). The keys are generated to conceal their construction and make it challenging to find the private key by only knowing the public key. The keys for the RSA algorithm are generated as follows.

• 1) Pick two large prime numbers, p, and q, p != q; 
• 2) Calculate n = p × q<the product n is used as the modulus for both public and private key>; 3) Calculate ø (n) = (p − 1)(q − 1) <where ø is Euler’s Totient function>; 
• 4) Pick e, so that gcd(e, ø (n)) = 1, 1 < e <  ø (n) <where e is public key>; 
• 5) Calculate d, so that d · e mod ø (n) = 1, i.e., d is the multiplicative inverse of e in mod  ø (n) <where d is a private key>; 
• 6) Get public key as KU = {e, n}; 
• 7) Get private key as KR = {d, n}.

2. Encryption:

A secret message to any person can be encrypted by their public key (that could be officially listed, like phone numbers). For plaintext block P < n, its ciphertext C = P^e (mod n).

3. Decryption:

The person addressed can easily decrypt the secret message using the private key. Its plaintext is P = C^d (mod n) for ciphertext block C.

Example of RSA Algorithm (Encryption and Decryption)

Key Generation: 1. Select primes: p=17 & q=11 2. Compute n = p*q =17×11=187 3. Compute ø(n)=(p–1).(q-1) =16×10=160 4. Select e: gcd(e,160) =1; choose e=7 5. Determine d: de=1 mod 160 and d < 160 Value is d=23 since 23×7=161= 10×160+1 6. Publish public key KU= {7,187} 7. Keep secret private key KR= {23,17,11} 8. sample RSA encryption/decryption is: 9. given message M = 88 (nb. 88<187) Encryption: 10. C = 887 mod 187 = 11 Decryption: 11. M = 1123 mod 187 = 88

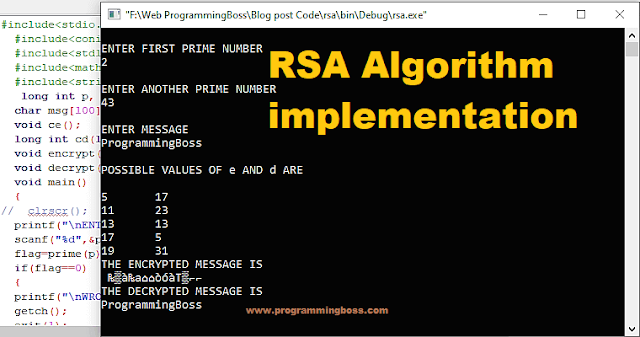
Implementing the RSA algorithm in C Program

The RSA algorithm is widely used for secure data encryption and digital signature. Here is an example of how RSA can be implemented in C:

The output of implemented program in C

RSA Algorithm (Encryption and Decryption) implementation in C

Conclusion:

The RSA algorithm is a widely used public key encryption technique that provides secure communication over an insecure network such as the Internet. It involves generating a public and private key, encrypting a message using the recipient's public key, and decrypting it using the recipient's private key. The RSA algorithm uses mathematical operations such as prime number generation, Euler's Totient function, and modular arithmetic. The security of RSA lies in the difficulty of factoring large prime numbers. Implementing the RSA algorithm in a C program can help secure data encryption and digital signature.

For More algorithms, please check here. 

Diffie Hellman Key exchange algorithm Implementation in C